Question

Find the ratio in which the lines segment joining A(1,-5) & B(-4,5) is divided by the x-axis. Also find the corrdinates of the point of the division.​

Answer 1

Explanation:

`\large\underline{\sf{Solution-}}`

Given that

A line segment AB having coordinates of A as (1, - 5) and coordinates of B as (- 4, 5).

Let assume that x - axis divides the line segment joining the points A (1, - 5) and B (- 4, 5) in the ratio k : 1 at C.

Let assume that coordinates of C be (x, 0).

We know,

Section formula :-

Let P(x₁, y₁) and Q(x₂, y₂) be two points in the coordinate plane and R(x, y) be the point which divides PQ internally in the ratio m₁ : m₂. Then, the coordinates of R will be:

`\sf\implies \boxed{\tt{ R = \bigg((m_(1)x_(2)+m_(2)x_(1))/(m_(1)+m_(2)), (m_(1)y_(2)+m_(2)y_(1))/(m_(1)+m_(2))\bigg)}}`

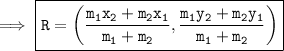
So, on substituting the values, we get

`\rm \longmapsto\:(x,0) = \bigg(( - 4k + 1)/(k + 1), \: (5k - 5)/(k + 1) \bigg)`

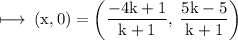
On comparing y - coordinate on both sides, we get

`\rm \longmapsto\:(5k - 5)/(k + 1) = 0`

`\rm \longmapsto\:5k - 5 = 0`

`\rm \longmapsto\:5k = 5`

`\bf\implies \:k = 1`

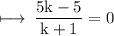
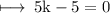
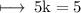
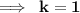
Hence,

The x - axis divides the line segment joining the points A (1, - 5) and B (- 4, 5) in the ratio 1 : 1 at C.

Now, On comparing x - coordinate on both sides, we get

`\rm \longmapsto\:x = ( - 4k + 1)/(k + 1)`

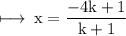
On substituting the value of k, we get

`\rm \longmapsto\:x = ( - 4+ 1)/(1 + 1)`

`\rm \longmapsto\:x \: = - \: (3)/(2)`

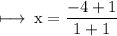
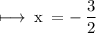
Hence,

The coordinates of point of intersection, C is

`\rm\implies \:\boxed{\tt{ Coordinates \: of \: C = \bigg( - (3)/(2), \: 0 \bigg) }}`