Substitute
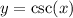 to rewrite the integral as
to rewrite the integral as
![\displaystyle I = \int_0^(\pi/2) \sqrt[5]{\tan(x)} (\ln(\csc^2(x)))/(\sin(2x)) \, dx \\\\ ~~~~ = \int_1^\infty (y \ln(y))/(\left(y^2-1\right)^(11/10)) \, dy](https://img.qammunity.org/2023/formulas/mathematics/college/8dkat2gxsifl9oib8w9u28rl704jgxab3t.png)
Substitute
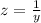 to rewrite again as
to rewrite again as
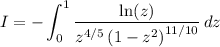
Substitute
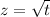 to rewrite to
to rewrite to
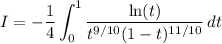
One last substitution of
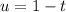 to rewrite
to rewrite
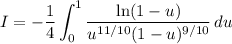
To summarize, substitute
 .
.
Now write the power series of
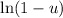 and evaluate the subsequent beta integral.
and evaluate the subsequent beta integral.
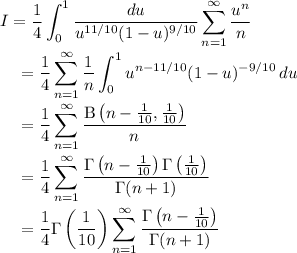
A lemma:

Recall the binomial series,
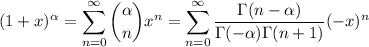
Let
 , so the left side vanishes. This means
, so the left side vanishes. This means
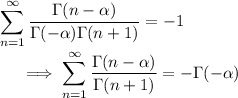
Let
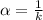 and use the identity
and use the identity
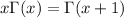 to write
to write
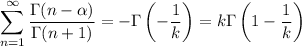
Let
 , so our integral is
, so our integral is
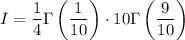
Recall the reflection formula,
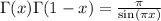 .
.
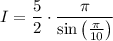
In an earlier question [28756378] we found the exact value
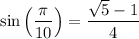
So we ultimately find that
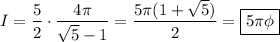
(Try saying that 5 times fast!)