Question

A bag contains five ​batteries, all of which are the same size and are equally likely to be selected. Each battery is a different brand. If you select four batteries at​ random, use the counting principle to determine how many points will be in the sample space if the batteries are selected

​a) with replacement.
​b) without replacement.

Answer 1

Answers:

a) 625

b) 120

=============================================

Step-by-step explanation:

If we select with replacement, then the first battery chosen is put back or we put a cloned copy in the bag. The contents of the bag have not changed. This means the second selection has the exact same identical situation as the first selection. By extension, any future selection has the same idea.

We have 5 batteries for any given selection, and we select 4 batteries. That gives 5*5*5*5 = 5^4 = 625 different outcomes in the sample space.

---------------

Now consider a situation where we don't apply replacement. Whatever is selected is not put back, and we don't put in a cloned copy. We go from 5 choices in the first selection, then 5-1 = 4 choices for the second, 5-2 = 3 choices for the third, and 5-3 = 2 choices for the fourth.

Overall there are 5*4*3*2 = 120 different outcomes in the sample space this time.

Another way to calculate this value is to plug n = 5 and r = 4 into the nPr permutation formula below

`nPr = (n!)/((n-r)!)`

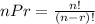
The exclamation marks represent factorials.