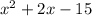Question

Write a quadratic equation whose roots are 3 and -5. Show your work using the Equation Editor Tool.

Answer 1

`{x}^(2) + 2x - 15`

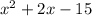
Explanation:

Since the roots are 3 & -5, we can write out the factors as binomials:

(x - 3)(x + 5)

If you set both to 0 & solve for x, you will get -5 & 3 as your roots.

From here we can FOIL to get a quadratic equation. Essentially, we are multiplying the first x & -3 by both the second x & 5 to get 4 terms (3 simplified).

This becomes:

`{x}^(2) + 5x - 3x - 15`

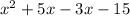
We can simplify the x to the 1st power terms to get our final equation:

`{x}^(2) + 2x - 15`