Answer:

Explanation:
sin²(x) = 1 - cos²(x)
So the expression sin²(x) + 7cosx +7 becomes
1 - cos²(x) + 7cos(x) + 7
Group like terms





Let's deal with the expression in parenthesis



This is of the form

with a = 1, b = -7 and c = -8
To factor this find two values u and v such that

If we choose u = 1 and v = -8 we can satisfy the above relationship since
u · v = 1 (-8) = -8 and u + v = 1 +(-8) = -7
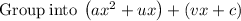



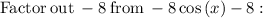
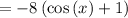
So

=

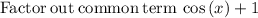

Since this was the term in the parenthesis with a leading negative sign, add the negative sign to get



Answer:
