1 Answer

Kbrimington · Answer 1 · 2023-12-19T16:14:22+0000

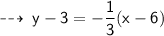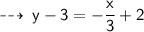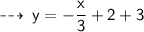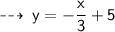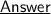
${ \qquad\qquad\huge\underline{{\sf Answer}}}$

Let's solve ~

The equation of line perpendicular to required line is :

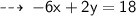
$\qquad \sf  \dashrightarrow \: - 6x + 2y = 18$

now, let's write it in alope intercept form to get its slope.

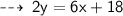
$\qquad \sf  \dashrightarrow \: 2y = 6x + 18$

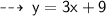
$\qquad \sf  \dashrightarrow \: y = 3x + 9$

so, slope of this line is 3, and we know that product of slopes of two perpendicular lines is -1.

So, slope of required line is :

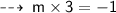
$\qquad \sf  \dashrightarrow \: m * 3 = - 1$

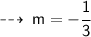
$\qquad \sf  \dashrightarrow \: m = - \cfrac{1}{3}$

Now, we know slope of required line ( i.e - 1/3 ) and ir goes through point (6 , 3), let's write it's equation in point slope form ~

$\qquad \sf  \dashrightarrow \: y - 3 = - ( 1)/(3) (x - 6)$

$\qquad \sf  \dashrightarrow \: y - 3 = - (x)/(3) + 2$

$\qquad \sf  \dashrightarrow \: y = - (x)/(3) + 2 + 3$

$\qquad \sf  \dashrightarrow \: y = - (x)/(3) + 5$

Please log in or register to add a comment.