The inequality representing the maximum number of gigabytes
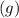 Yusuf can use while staying within his budget is
Yusuf can use while staying within his budget is
 . Since
. Since
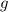 must be a whole number, Yusuf can use at most 3 gigabytes to stay within his budget.
must be a whole number, Yusuf can use at most 3 gigabytes to stay within his budget.
Let
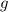 be the number of gigabytes Yusuf uses. The total cost
be the number of gigabytes Yusuf uses. The total cost
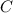 is given by the flat cost plus the cost per gigabyte:
is given by the flat cost plus the cost per gigabyte:
![\[ C = 57 + 5g \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/5c15sx0vuh48nrl6ao7vmp2k5jk0ud3odg.png)
Yusuf wants to keep his bill under $75, so the inequality for his budget constraint is:
![\[ C \leq 75 \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/rsoagwhuzicpd1gzl037nh8mfxfcl9juws.png)
Substitute the expression for
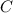 :
:
![\[ 57 + 5g \leq 75 \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/jf8azo7k0y3fbah8buv1q0bgggcbqy2nlc.png)
Now, you can solve for
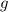 to find the maximum number of gigabytes Yusuf can use while staying within his budget. Subtract 57 from both sides:
to find the maximum number of gigabytes Yusuf can use while staying within his budget. Subtract 57 from both sides:
![\[ 5g \leq 18 \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/476xbz2vjpbfabyx2z0ck68qm9gxxo377i.png)
Divide both sides by 5:
![\[ g \leq 3.6 \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/aj55jyf3e9yo2d6xg2r8ieojvr44pq20ca.png)
So, the inequality representing the maximum number of gigabytes
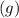 Yusuf can use while staying within his budget is
Yusuf can use while staying within his budget is
 . Since
. Since
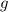 must be a whole number, Yusuf can use at most 3 gigabytes to stay within his budget.
must be a whole number, Yusuf can use at most 3 gigabytes to stay within his budget.