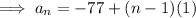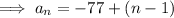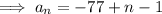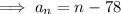Answer:
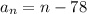
Explanation:
Given sequence:
-77, -76, -75, -74, ...
This is an arithmetic sequence as the difference between each term is the same.
General form of an arithmetic sequence

Where:
 is the nth term.
is the nth term.
 is the first term.
is the first term.
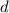 is the common difference between terms.
is the common difference between terms.
 is the position of the term.
is the position of the term.
To find the common difference (d), subtract consecutive terms:
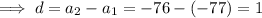
Substitute the first term and the found common difference into the formula to create an equation for the nth term: