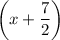Question

If x +2 is a factor of p(x) =x²-kx +7, thrn find the value of k.Also,find the other factor of the polynomial ?​

Answer 1

`k=-(11)/(2)`

`\left(x+(7)/(2)\right)`

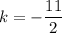
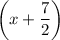
Explanation:

`\boxed{\begin{minipage}{5.7 cm}\underline{Factor Theorem}\\\\If f$(x)$ is a polynomial, and f$(a) = 0$,\\then $(x-a)$ is a factor of f$(x)$.\end{minipage}}`

Given polynomial function:

`p(x)=x^2-kx+7`

Apply the Factor Theorem:

`\begin{aligned} \textsf{If $(x + 2)$ is a factor of $p(x)$ then: \quad}p(-2)&=0\\\\\implies (-2)^2-k(-2)+7&=0\\4+2k+7&=0\\2k+11&=0\\2k&=-11\\k&=-(11)/(2)\end{aligned}`

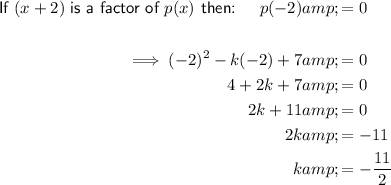
Substitute the found value of k into the original function:

`\implies p(x)=x^2-\left(-(11)/(2)\right)x+7`

`\implies p(x)=x^2+(11)/(2)x+7`

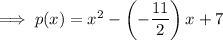
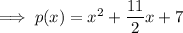
As (x + 2) is factor of the polynomial, and the leading coefficient of the function is 1, the other factor will be (x + q) where q is a constant to be found.

`\begin{aligned}x^2+(11)/(2)x+7 & = (x+2)(x+q)\\& = x^2+qx+2x+2q\\& = x^2+(2+q)x+2q \end{aligned}`

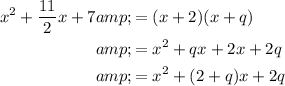
Compare the constant of the given polynomial with the constant of the expanded factors:

`\implies 2q=7`

`\implies q=(7)/(2)`

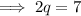
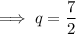
Therefore:

`\implies x^2+(11)/(2)x+7 = (x+2)\left(x+(7)/(2)\right)`

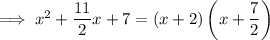
So the other factor of the given polynomial is:

`\left(x+(7)/(2)\right)`