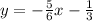Answer:
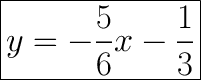
Useful Information:
The equation of a straight line:

Explanation:
To work this out you would first need to substitute the gradient into the equation, this gives you
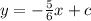 .
.
The next step is to substitute the x and y coordinates from the point (2,-2) into the equation, this gives you
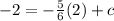
In order to work out the value of c, you would have to bring the value of
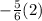 over to the other side, this can be done by adding
over to the other side, this can be done by adding
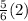 or
or
 to -2, which gives you
to -2, which gives you
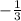 .
.
The final step is to substitute the m value of
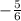 and the c value of
and the c value of
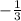 into the equation, this gives you
into the equation, this gives you
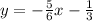
1) Substitute the gradient.
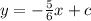
2) Substitute the x and y coordinates.
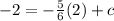
3) Bring
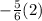 over to the other side.
over to the other side.

4) Simplify to find the value of c.

5) Substitute the m and c values.