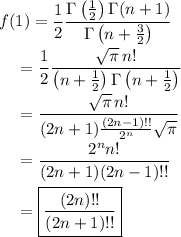Consider the function
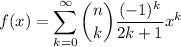
Note that
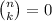 when
when
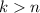 , so our sum is exactly
, so our sum is exactly
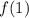 .
.
Let
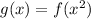 . Then
. Then
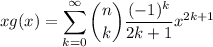
and differentiating both sides reduces the sum to a binomial series,
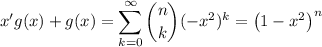
Solve the differential equation for
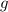 . Since
. Since
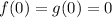 , by the fundamental theorem of calculus we have
, by the fundamental theorem of calculus we have
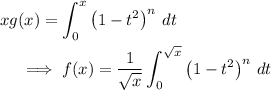
Let
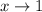 from below.
from below.
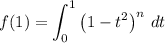
Substitute
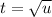 and
and
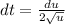 to transform this to a beta function integral.
to transform this to a beta function integral.
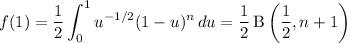
Now we just employ a few beta-gamma and gamma-factorial identities to simplify this result.
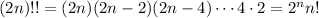
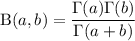
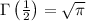

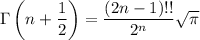
It follows that