Recalling the Mittag-Leffler expansion for the hyperbolic cotangent,

which, by symmetry, is the same as
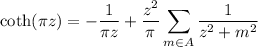
where
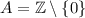 .
.
By symmetry again, the given sum is

Now rewrite the summand using the M-L expansion.
![\displaystyle S = \frac12 \sum_(n\in A) \frac1{n^3} \left(-\frac1{\pi nx} + \frac{n^2x^2}\pi \sum_(m\in A) \frac1{n^2x^2+m^2} - \frac x{\pi n} + (n^2)/(\pi x^2) \sum_(m\in A) \frac1{(n^2)/(x^2) + m^2}\right) \\\\ = -\frac1{2\pi x} \left[(x^3+1)\sum_(n\in A)\frac1{n^4} - x^3 \sum_((m,n)\in A^2) \frac1n\cdot\frac1{n^2x^2+m^2} - x^2 \sum_((m,n)\in A^2) \frac1n\cdot\frac1{m^2x^2+n^2}\right]](https://img.qammunity.org/2023/formulas/mathematics/college/p4j5inbyq7x8b0w19jap8zmrjri3hpibtq.png)
By symmetry,

and recalling the definition of the Riemann zeta function, this brings us to
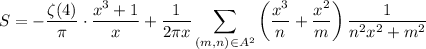
and that's unfortunately as far as I've gotten...