Question

Write the equation of the line in slope-intercept form that passes through the points (4, 2) and (-3, 2).

Answer 1

`y=2`

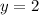
Explanation:

We can find the slope of the equation using the slope formula:
`m=(y_2-y_1)/(x_2-x_1)`

So let's say that:
`(x_1, y_1)=(4, 2)\text{ and }(x_2, y_2)=(-3, 2)`

Plugging in the values into the equation we get:
`(2-2)/(-3-4)=(0)/(-7)=0`

The slope is just zero, and we could substitute values into the slope formula, but we just know that it's a hori
`y=0x+2\to y=2`zontal line since there is no change in y, and it has to pass through the y-value of 2, thus the only possible equation is:
`y=2`

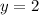
But let's say this wasn't the case, we can still plug values into the slope-intercept equation:
`y=mx+b` where m=slope, and b=y-intercept that we want to solve for

Let's use the point (4, 2) to plug in as (x, y)

`2=4(0)+b`

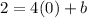
this will just simplify to

`2=b`

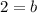
and plugging this into our slope-intercept form equation form we just get: