Question

1. The graph of f. consisting of three line segments, is given to the right. Let g(x) = $* f (t)dt. a. Compute g(4) and g(-2)(Need help on C and D)​

Answer 1

Hi there!

c.

Looking at the graph, we can eliminate any possibility of t values on the positive t-axis being an absolute minimum. The only sign change in this interval is from positive to negative, which indicates a maximum.

We can find the value of t = -2 using the integral:

`g(-2) = \int\limits^(-2)_1 {f(t)} \, dt`

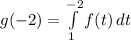
Rewrite in proper format:

`g(-2) = -\int\limits^1_(-2){f(t)} \, dt`

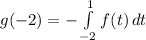
Solve using the graph:

`g(-2) = -(1)/(2)bh = -(1)/(2)(3 \cdot 4) = -6`

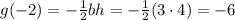
There is an absolute minimum value of g at x = -2. Using the above integral, we get a value of g(-2) = -6, which is the lowest value attainable over the interval.

d.

There is an inflection point at x = 1 because the second derivative changes from positive to negative at this value. (Changes signs). There is NOT an inflection point at x = 2 because the second derivative remains negative, although with a different value.