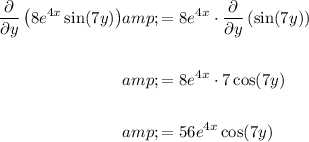Question

Calculate the partial derivatives of a function of two variables.

Answer 1

`(\partial f)/(\partial x) =\boxed{32e^(4x) \sin (7y)}`

`(\partial f)/(\partial y) =\boxed{56e^(4x)\cos (7y)}`

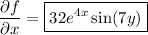
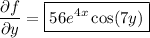
Explanation:

Partial derivatives measure the rate at which a multivariable function changes with respect to one of its variables while keeping the other variables constant.

Given multivariable function:

`f(x,y)=8e^(4x) \sin(7y)`

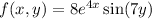
To find the partial derivative δf/δx, differentiate f with respect to x, whilst treating y as a constant.

Take out the constant 8sin(7y):

`(\partial )/(\partial x)\left(8e^(4x) \sin(7y)\right)=8 \sin(7y) \cdot (\partial )/(\partial x)\left(e^(4x)\right)`

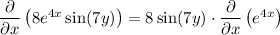
Now, use the following differentiation rule:

`\boxed{\begin{array}{c}\underline{\textsf{Differentiating $e^(f(x))$}}\\\\\frac{\text{d}}{\text{d}x}\:e^(f(x))=f\:'(x)\cdot e^(f(x))\end{array}}`

Therefore:

`\begin{aligned}(\partial )/(\partial x)\left(8e^(4x) \sin(7y)\right)&=8 \sin(7y) \cdot (\partial )/(\partial x)\left(e^(4x)\right)\\\\&=8 \sin(7y) \cdot4 \cdot e^(4x)\\\\&=32e^(4x)\sin(7y)\end{aligned}`

To find the partial derivative δf/δy, differentiate f with respect to y, whilst treating x as a constant.

Take out the constant
`8e^(4x)`:

`(\partial )/(\partial y)\left(8e^(4x) \sin(7y)\right)=8 e^(4x) \cdot (\partial )/(\partial y)\left(\sin(7y)\right)`

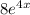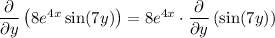
Now, use the following differentiation rule:

`\boxed{\begin{array}{c}\underline{\textsf{Differentiating $\sin(kx)$}}\\\\\frac{\text{d}}{\text{d}x}\:\sin(kx)=k\cos(kx)\end{array}}`

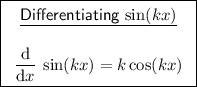
Therefore:

`\begin{aligned}(\partial )/(\partial y)\left(8e^(4x) \sin(7y)\right)&=8 e^(4x) \cdot (\partial )/(\partial y)\left(\sin(7y)\right)\\\\&=8e^(4x)\cdot 7\cos (7y)\\\\&=56e^(4x)\cos(7y)\end{aligned}`