Question

Help me with number 59 and 60 :)

Answer 1

59. a₁ = 4

60. a₁ = 10

Explanation:

The general equation for the sum of the first n terms Sₙ of a geometric sequence with common ratio r and first term a₁ is

`S_n = a_1 (1-r^n)/(1-r)`

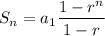
Problem 59

Here we are given

`S_n = (31)/(4)\\\\r = (1)/(2)`

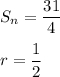
So we can plug these values into the above equation and get
`a_1`

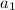
Let's first compute
`1 - r^n`

`1 - r^n = 1 - \left((1)/(2)\right)^5\\\\\left((1)/(2)\right)^5 = (1)/(32)\\\\1 - r^n = 1 - \left((1)/(2)\right)^5 = 1-(1)/(32) = (32)/(32)-(1)/(32) = (31)/(32)`

`1- r = 1 - (1)/(2) = (1)/(2)`

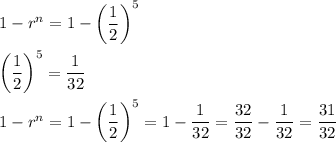
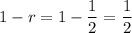
So

`(1-r^n)/(1-r) = (31)/(32) / (1)/(2) = (31)/(32) * (2)/(1) = (31)/(16)`

Substituting this value into
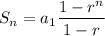`S_n = a_1 (1-r^n)/(1-r)` we get

`(31)/(4) = a_1(31)/(16)`

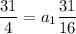
Multiplying both sides by
`(16)/(31)`

`(31)/(4) *(16)/(31) = a_1(31)/(16) *(16)/(31)\\\\4 = a_1 \textrm{or alternatively }\\ \\\boxed{a_1 = 4}`

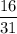
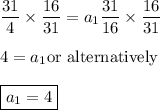
Problem 60

Use the same technique as above

`S_8 = 2550, r = 2\\\\S_8 = a_1 * (1-r^8)/(1-r)\\\\\\2550 = a_1 * (1-2^8)/(1-2)\\\\2550 = a_1 * (1 - 256)/(1-2)\\\\2550 = a_1 * (-255)/(-1)\\\\2550 = a_1 *255\\\\== > a_1 = (2550)/(255)\\\\\boxed{a_1=10}`