Question

Determine whether the quadratic function shown below has a minimum or

maximum, then determine the minimum or maximum value of the functio
ƒ(x) = x² + 6x + 7

Answer 1

Minimum = (-3, -2)

Explanation:

Standard form of a quadratic function:

`f(x)=ax^2+bx+c`

If a > 0 the parabola opens upwards and the curve has a minimum point.

If a < 0 the parabola opens downwards and curve has a maximum point.

Given function:

`f(x)=x^2+6x+7`

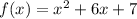
As a > 0, the parabola opens upwards and so the curve has a minimum point.

The minimum/maximum point of a quadratic function is its vertex.

Vertex form of a quadratic function:

`f(x)=(x-h)^2+k`

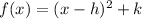
Where (h, k) is the vertex.

To rewrite the given function in vertex form, complete the square.

Add and subtract the square of half the coefficient of the term in x:

`\implies f(x)=x^2+6x+7 +\left((6)/(2)\right)^2-\left((6)/(2)\right)^2`

`\implies f(x)=x^2+6x+7 +9-9`

`\implies f(x)=x^2+6x+9+(7 -9)`

`\implies f(x)=x^2+6x+9-2`

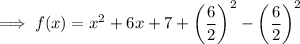
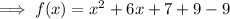
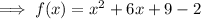
Factor the perfect square trinomial formed by x²+6x+9:

`\implies f(x)=(x+3)^2-2`

Compare with the vertex form:

• h = -3
• k = -2

Therefore, the vertex is (-3, -2) and so the minimum value of the given function is (-3, -2).