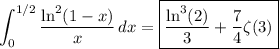Substitute
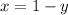 and
and
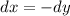 .
.
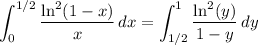
Since
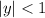 , we can expand into a power series and interchange the integral with the sum.
, we can expand into a power series and interchange the integral with the sum.
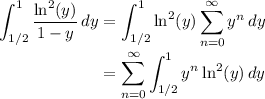
Let
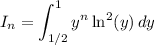
Integrate by parts with
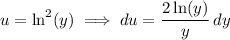
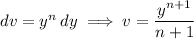
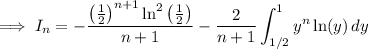
Integrate by parts again, now with
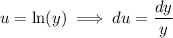
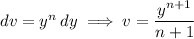
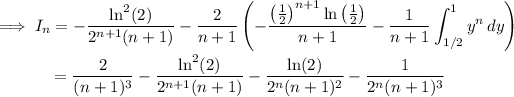
Taking the sum over all
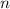 gives
gives
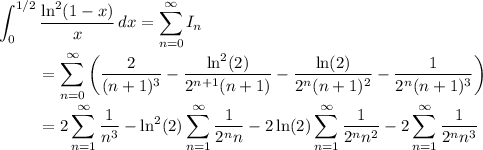
Now recall the definition of the so-called polylogarithm function, given by
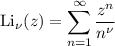
which immediately gives us a "closed" form for the integral of
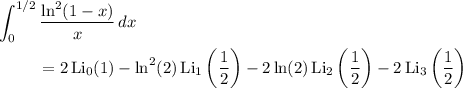
But we can do better. The first sum is
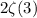 (by definition of Riemann zeta) and the second is
(by definition of Riemann zeta) and the second is
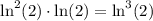 (using the series expansion of
(using the series expansion of
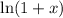 ). The other two polylogs have exact values of
). The other two polylogs have exact values of
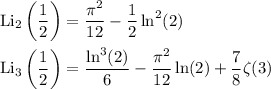
(according to what I found when searching "polylogarithm at half integers"). Putting all the results together, we end up with