Question

Consider the waited voting system

[34: 9,9,6,6,6,6,5]
Find the weight of the coaltion {p1,p3,p4}

Answer 1

Answer: 21

=======================================================

Step-by-step explanation:

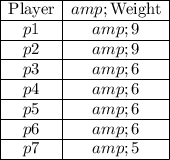
The values after the colon are 9,9,6,6,6,6,5

They are the weights of players p1 through p7

• Player p1 has 9 votes
• Player p2 has 9 votes
• Player p3 has 6 votes
• Player p4 has 6 votes
• Player p5 has 6 votes
• Player p6 has 6 votes
• Player p7 has 5 votes

It might help to make a table like this

`\begin{array}c \cline{1-2}\text{Player} & \text{Weight}\\\cline{1-2}p1 & 9\\\cline{1-2}p2 & 9\\\cline{1-2}p3 & 6\\\cline{1-2}p4 & 6\\\cline{1-2}p5 & 6\\\cline{1-2}p6 & 6\\\cline{1-2}p7 & 5\\\cline{1-2}\end{array}`

The coalition {p1,p3,p4} is the set of these voters teaming up to pool together 9+6+6 = 21 votes.

--------------

Extra info:

There are 9+9+6+6+6+6+5 = 47 votes total.

The 34 represents the quota. It's between 47/2 = 23.5 and 47

In other words, q = 34 makes the inequality
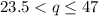`23.5 < q \le 47` true, and this helps show we have a valid weighted voting system.

This quota q = 34 the minimum number of votes needed to pass the measure. Since the coalition {p1,p3,p4} can only get 20 votes, this combined weight is not over the threshold to pass the measure the coalition is in favor of (or block the measure they are against). We consider it a losing coalition. They'll need more voters to join the coalition.

For more information, check out the concept "Banzhaf Power Index".