1) 8 + 3x < 2
To solve this, you first want to subtract 8 from both sides to isolate 3x on one side.
This gives you 3x < 2 - 8, which can be simplified to 3x < -6.
After you have this, you want to get x on its own. To do this, divide both sides of the inequality by 3 to get x < -6
2) 2x + 23
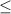 11
11
For this one, we use the same steps. First, subtract 23 from both sides to isolate 2x, giving us 2x
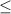 11 - 23, which we simplify down to 2x
11 - 23, which we simplify down to 2x
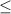 -12.
-12.
From here, we divide both sides of the inequality by 2 to get x on its own. This gives us x
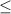 -6
-6