Question

A ball rolls off a table with a horizontal velocity of 4 m/s. If it takes 0.5 seconds for the ball to reach the floor, how high above the floor kd tje tabletop? (Use g = 10 m/s^2)

Show work please :)​

Answer 1

1.25 m

Step-by-step explanation:

Constant Acceleration Equations (SUVAT)

`\boxed{\begin{array}{c}\begin{aligned}v&=u+at\\\\s&=ut+(1)/(2)at^2\\\\ s&=\left((u+v)/(2)\right)t\\\\v^2&=u^2+2as\\\\s&=vt-(1)/(2)at^2\end{aligned}\end{array}} \quad \boxed{\begin{minipage}{4.6 cm}$s$ = displacement in m\\\\$u$ = initial velocity in ms$^(-1)$\\\\$v$ = final velocity in ms$^(-1)$\\\\$a$ = acceleration in ms$^(-2)$\\\\$t$ = time in s (seconds)\end{minipage}}`

When using SUVAT, assume the object is modeled as a particle and that acceleration is constant.

Consider the horizontal and vertical motion of the ball separately.

As the ball rolls off the table with a horizontal velocity only, the vertical component of its initial velocity is zero.

Acceleration due to gravity = 10 ms⁻²

As we need to find the vertical displacement of the ball, resolve vertically, taking ↓ as positive:

`u=0 \quad a=10 \quad t=0.5`

`\begin{aligned}\textsf{Using} \quad s&=ut+(1)/(2)at^2\\\\s&=(0)(0.5)+(1)/(2)(10)(0.5)^2\\s&=0+(1)/(2)(10)(0.25)\\s&=(5)(0.25)\\ \implies s&=1.25 \; \sf m\end{aligned}`

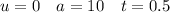
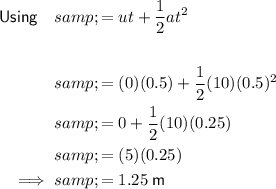
Therefore, the vertical displacement of the ball is 1.25 m, and so the table is 1.25 m above the floor.