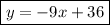Question

the points (4,0) and (3,9) lie on a particular line. which is its equation in slope intercept form of this line

Answer 1

`y = -9x + 36`

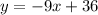
Explanation:

`\textsf {The slope-intercept form of a line is $y = mx + b$ where m is the slope and b the y-intercept}\\ \\\textsf{Slope is computed using the formula}`

`m = \frac {(y_(2) - y_(1))} {(x_(2) - x_(1))}`

`\sf where \; (x_1,y_1) and (x_2, y_2)\; are\;any\;two\;points\;on\;the\;line`

`\textsf{Given that the line passes through (4, 0) and (3, 9) we can compute the slope:}`

`m = (9 - 0)/(3 - 4)\\\\m = (9)/(-1)\\\\m = -9`

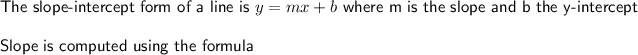
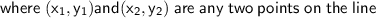
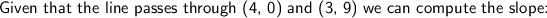
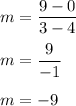
So the slope of the line is y = -9x + b

We have
y = -9x + b

Add 9x to both sides

y + 9x = -9x + 9x + b

y + 9x = b

switching sides,

b = y + 9x

Plug in the (x, y) values for point (4, 0)

b = 0 + 9(4)

b = 36

So the equation of the line is

`\boxed{y = -9x + 36}`