Answer:
Explanation:
Let the first GP is:
Use the sum formula:
Now, the second GP:
Its sum is:
Compare the S₁ and S₂:
- a/(1 - r) = 2 ⇒ a= 2(1 - r)
- a³/(1 - r³) = 32/13 ⇒ a³ = 32/13(1 - r³)
Substitute the value of a into this equation:
- (2(1-r))³ = 32/13(1 - r³)
- (1 - r)³ = 4/13(1 - r³)
- 13(1 - r)(1- r)² = 4(1 - r) (1 + r + r²)
- r₁ = 1, one of the roots, cancel (1 - r) on both sides
- 13(1 - 2r + r²) = 4(1 + r + r²)
- 13 - 26r + 13r² = 4 + 4r + 4r²
- 9r² - 30r + 9 = 0
- 3r² - 10r + 3 = 0
- r = (10 ±
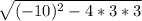 )/6 = (10 ± 8)/6
)/6 = (10 ± 8)/6 - r₂ = 3, r₃ = 1/3
Find respective values of a:
- r₁ = 1 ⇒ a = 2(1 - 1) = 0, this ends up with no GP
- r₂ = 3 ⇒ a = 2(1 - 3) = -4, this is discounted as well since r > 1
- r₃ = 1/3 ⇒ a = 2(1 - 1/3) = 4/3