Question

Given the Infinite Geomerric Series which has the sum of 2 and the sum of cube of each terms in this series results in a new Infinite Geometric Series which has the sum of 32/13. Find the first term 'a' and common ratio 'r' of the first/intial Infinite Geometric Series. Please show your work too — thanks!

Answer 1

• See below

Explanation:

Let the first GP is:

• a, ar, ar², ...

Use the sum formula:

• S₁ = a/ (1 - r) = 2

Now, the second GP:

• a³, (ar)³, (ar²)³, ...

Its sum is:

• S₂ = a³/(1 - r³) = 32/13

Compare the S₁ and S₂:

• a/(1 - r) = 2 ⇒ a= 2(1 - r)
• a³/(1 - r³) = 32/13 ⇒ a³ = 32/13(1 - r³)

Substitute the value of a into this equation:

• (2(1-r))³ = 32/13(1 - r³)
• (1 - r)³ = 4/13(1 - r³)
• 13(1 - r)(1- r)² = 4(1 - r) (1 + r + r²)

• r₁ = 1, one of the roots, cancel (1 - r) on both sides

• 13(1 - 2r + r²) = 4(1 + r + r²)
• 13 - 26r + 13r² = 4 + 4r + 4r²
• 9r² - 30r + 9 = 0
• 3r² - 10r + 3 = 0
• r = (10 ±
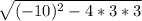  `√((-10)^2-4*3*3)`)/6 = (10 ± 8)/6
• r₂ = 3, r₃ = 1/3

Find respective values of a:

• r₁ = 1 ⇒ a = 2(1 - 1) = 0, this ends up with no GP
• r₂ = 3 ⇒ a = 2(1 - 3) = -4, this is discounted as well since r > 1
• r₃ = 1/3 ⇒ a = 2(1 - 1/3) = 4/3