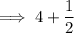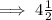(1)/(4)(15-6) + 3^(3) divided by 12 A) 2(1)/(2) B) 3 C) 4(1)/(2) D) 5(7)/(12)

Question

`(1)/(4)(15-6) + 3^(3)` divided by 12

A)
`2(1)/(2)`

B) 3

C)
`4(1)/(2)`

D)
`5(7)/(12)`

Answer 1

C)
`\sf 4(1)/(2)`

Explanation:

The given equation is,

`\sf \: → (1)/(4) (15 - 6) + \frac{ {3}^(3) }{12}`

The value of the equation is,

`\sf \rightarrow (1)/(4) (15 - 6) + \frac{ {3}^(3) }{12}`

`\sf \: \rightarrow (1)/(4) (9) + (27)/(12)`

`\sf → (9)/(4) + (27)/(12)`

`\sf → ((27 + 27))/(12)`

`\sf → ((54 / 6))/((12 / 6))`

`\sf → (9)/(2) = 4 (1)/(2)`

Hence, the required value is 4 1/2.

Answer 2

`\textsf{C)} \quad 4(1)/(2)`

Explanation:

PEMDAS

The PEMDAS rule is an acronym representing the order of operations in math:

• Parentheses
• Exponents
• Multiplication and Division (from left to right)
• Addition and Subtraction (from left to right)

Given expression:

`(1)/(4)(15-6)+(3^3)/(12)`

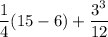
Carry out the operation inside the parentheses:

`\implies (1)/(4)(9)+(3^3)/(12)`

Carry out the exponent:

`\implies (1)/(4)(9)+(3 \cdot 3 \cdot 3)/(12)`

`\implies (1)/(4)(9)+(9 \cdot 3)/(12)`

`\implies (1)/(4)(9)+(27)/(12)`

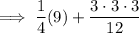
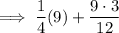
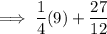
Carry out the multiplication:

`\implies (9)/(4)+(27)/(12)`

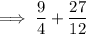
Rewrite 27 as 3 · 9 and 12 as 3 · 4:

`\implies (9)/(4)+(3 \cdot 9)/(3 \cdot 4)`

Cancel the common term 3:

`\implies (9)/(4)+(9)/(4)`

`\textsf{Apply the fraction rule} \quad (a)/(c)+(b)/(c)=(a+b)/(c):`

`\implies (9+9)/(4)`

`\implies (18)/(4)`

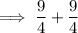
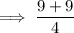
Reduce the fraction by dividing the numerator and denominator by 2:

`\implies (18 / 2)/(4 / 2)`

`\implies (9)/(2)`

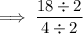
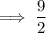
Rewrite 9 as 8 + 1:

`\implies (8+1)/(2)`

`\textsf{Apply the fraction rule} \quad (a+b)/(c)=(a)/(c)+(b)/(c):`

`\implies (8)/(2)+(1)/(2)`

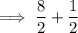
Divide 8 by 2:

`\implies 4+(1)/(2)`

`\implies 4(1)/(2)`