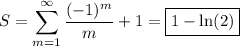Assuming the correction I suggested in comments, our sum is
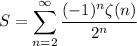
Rewrite with the definition of the Riemann zeta function, and condense the subsequent double series.
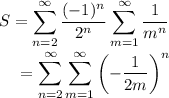
The condition for Fubini's theorem is met so we can interchange the sums.
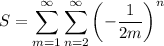
Sum the geometric series.
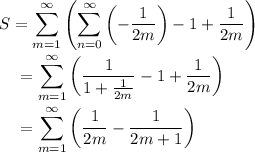
Considering the terms in the summand as even/odd parts, we can condense this further to the alternating series
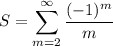
and recalling the power series
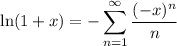
we let
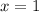 ; it follows that
; it follows that