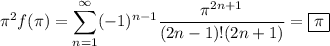Question

`\rm\sum_(n = 1)^ \infty ( - 1 {)}^(n - 1) \frac{ {\pi }^(2n + 1) }{(2n - 1)!(2n + 1)} \\` ​

Answer 1

Let

`\displaystyle f(x) = \sum_(n=1)^\infty (-1)^(n-1) (x^(2n-1))/((2n-1)! (2n+1))`

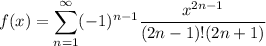
The exponent is indeed
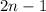`2n-1` - not a typo!

Take the antiderivative of
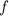`f`, denoted by
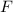`F`. This recovers a factor of
`2n` in the denominator, which lets us condense it to a single factorial.

`\displaystyle F(x) = \int f(x) \, dx = C + \sum_(n=1)^\infty (-1)^(n-1) (x^(2n))/((2n+1)!)`

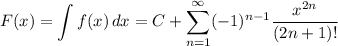
Recall the series expansion of sine,

`\displaystyle \sin(x) = \sum_(n=0)^\infty (-1)^n (x^(2n+1))/((2n+1)!)`

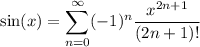
Then with a little algebraic manipulation, we get

`\displaystyle F(x) = \int f(x) \, dx = C + 1 - \frac{\sin(x)}x`

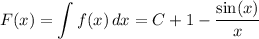
Differentiate to recover
`f`.

`f(x) = (\sin(x) - x\cos(x))/(x^2)`

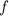Finally,
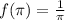`f(\pi) = \frac1\pi`, so our sum is

`\displaystyle \pi^2 f(\pi) = \sum_(n=1)^\infty (-1)^(n-1) (\pi^(2n+1))/((2n-1)! (2n+1)) = \boxed{\pi}`