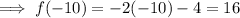Question

I don't Know how to solve this please help

Answer 1

f(0) = 0

f(-2) = 0

f(5) = 15

f(-10) = 16

Explanation:

Piecewise functions have multiple pieces of curves/lines where each piece corresponds to its definition over an interval.

Given piecewise function:

`f(x)=\begin{cases} \begin{aligned}-2x-4 & \;\;\textsf {if }\;x < 0\\3x & \;\;\textsf {if }\;x\geq 0\\\end{aligned}\end{cases}`

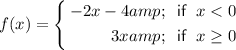
Therefore, the function has two definitions:

• 
  `\textsf{$f(x)=-2x-4$ when $x$ is less than zero}.`

• 
  `\textsf{$f(x)=3x$ when $x$ is more than or equal to zero}.`

When graphing piecewise functions:

• Use an open circle where the value of x is not included in the interval.
• Use a closed circle where the value of x is included in the interval.
• Use an arrow to show that the function continues indefinitely.

First piece of the function

Substitute zero into the first function:

`\implies f(0)=-2(0)-4=-4`

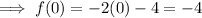
Place an open circle at point (0, -4).

To help graph the line, find another point on the line by inputting another value of x that is less than zero into the same function:

`\implies f(-2)=-2(-2)-4=0`

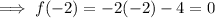
Place point (-2, 0) and draw a straight line from the open circle at (0, -4) through (-2, 0). Add an arrow at the other endpoint to show it continues indefinitely as x → -∞.

Second piece of the function

Substitute zero into the second function:

`\implies f(0)=3(0)=0`

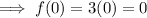
Place an closed circle at point (0, 0).

Again, to help graph the line, find another point on the line by inputting another value of x that is more than zero into the same function:

`\implies f(2)=3(2)=6`

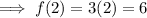
Place point (2, 6) and draw a straight line from the closed circle at (0, 0) through (2, 6). Add an arrow at the other endpoint to show it continues indefinitely as x → ∞.

See attached for graph.

To find the given functions, decide which function to use based on the given value of x, then solve.

f(0) means to find the value of the function when x = 0.

Therefore, input x = 0 into the second function as x ≥ 0.

`\implies f(0)=3(0)=0`

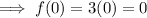
f(-2) means to find the value of the function when x = -2.

Therefore, input x = -2 into the first function as x < 0.

`\implies f(-2)=-2(-2)-4=0`

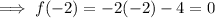
f(5) means to find the value of the function when x = 5.

Therefore, input x = 5 into the second function as x ≥ 0.

`\implies f(5)=3(5)=15`

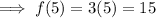
f(-10) means to find the value of the function when x = -10.

Therefore, input x = -10 into the first function as x < 0.

`\implies f(-10)=-2(-10)-4=16`