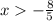Answer:
for (−4/5)x + 3/10 < 8/10: solution is x > -5/8
for −4/(5x) + 3/10 < 8/10: solution is x > -8/5
Explanation:
I'm not exactly sure if you mean -4 divided by 5x or (-4/5)x, so I've done both! :)
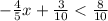
subtract 3/10 from both sides:
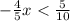
Divide both sides by 4/5:
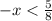
Divide both sides by -1 (reverse sign):
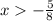
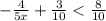
subtract 3/10 from both sides:
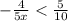
Multiply both sides by 5x:
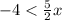
Divide both sides by 5/2: