1) Solve each inequality individually.
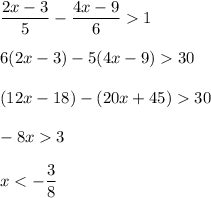
and
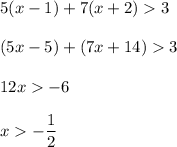
Then the solution set is
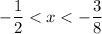
since -1/2 = -4/8 is smaller than -3/8.
2)
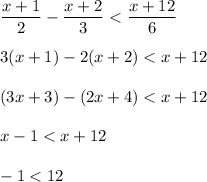
This is true for all values of
 .
.
For the second inequality, (I use periods in place of commas because it renders better as TeX)
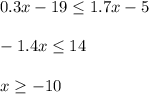
Taken together, the solution set is

3)
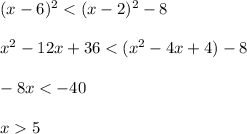
and
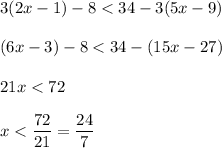
But
 cannot be both larger than 5 = 35/7 and smaller than 24/7, so there are no solutions.
cannot be both larger than 5 = 35/7 and smaller than 24/7, so there are no solutions.
4)
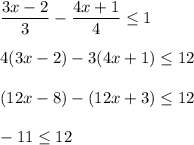
This is true for all
 .
.
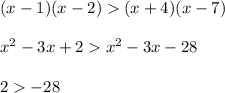
This is also true for all
 .
.
Any value of
 is a solution.
is a solution.