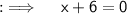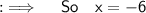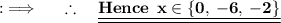Question

X^2(x+2)(x+6)=0
What are the solutions to the equation?

Answer 1

3 solutions

Explanation:

x = 0; x = 2; x = -6

Answer 2

As we are given with an equation as follows :

`{:\implies \quad \sf x^(2)(x+2)(x+6)=0}`

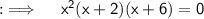
As product of these three factors is equal . So , any of these factor can be 0 as product is 0 only when one of the expressions which are multiplied is 0. So , 3 cases arises as follows ;

Case I :-

`{:\implies \quad \sf x^(2)=0}`

On raising ½ power to both sides we have ;

`{:\implies \quad \sf x=\pm \: 0}`

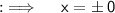
Now , as +0 and -0 have no difference in them . So , it's simply 0

`{:\implies \quad \sf So\quad x=0}`

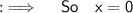
Case II :-

`{:\implies \quad \sf x+2=0}`

`{:\implies \quad \sf So\quad x=-2}`

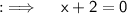
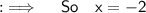
Case III :-

`{:\implies \quad \sf x+6=0}`

`{:\implies \quad \sf So\quad x=-6}`

`{:\implies \quad \bf \therefore \quad \underline{\underline{Hence \:\: x\in \{0,\: -6,\: -2\}}}}`