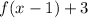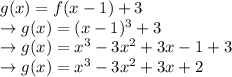Answer:
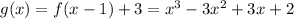
Explanation:
g(x) is f(x) moved one to the right, as well as moved 3 up (The inflection point was (0,0) on f(x), and is now at (1, 3) at g(x)).
Therefore, to move f(x) one to the right, we must subtract 1 from x, making it
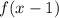 , and add 3 to the y value, making it
, and add 3 to the y value, making it