Answer:
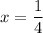
Explanation:
Given equation:
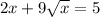
Subtract 2x from both sides to isolate the square root:
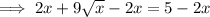
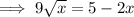
Square both sides to eliminate the square root:
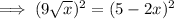
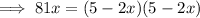
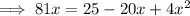
Subtract 81x from both sides:
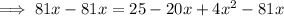

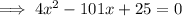
To factor a quadratic in the form
 , find two numbers that multiply to
, find two numbers that multiply to
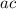 and sum to
and sum to
 :
:
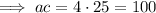
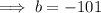
Therefore, the two numbers are -1 and -100 as:
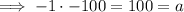
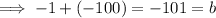
Rewrite
 as the sum of these two numbers:
as the sum of these two numbers:

Factor the first two terms and the last two terms separately:

Factor out the common term (4x - 1):
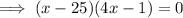
Apply the zero-product property:
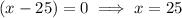
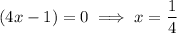
Input each solution into the original equation to check its validity:

Therefore, x = 25 is not a valid solution.
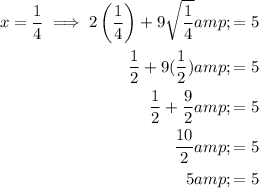
Therefore x = ¹/₄ is a valid solution.
Therefore, the only valid solution to the equation is x = ¹/₄.