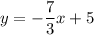Answer:
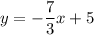
Explanation:
The general equation of a line in slope-intercept form is
y = mx + b
where m = slope and b = y-intercept is rise over run
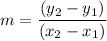
where (x₁, y₁) and (x₂, y₂) are any two points on the line
For the line passing through (-6, 19) and (3, -2) , the slope
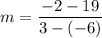
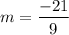
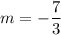
So slope-intercept form is
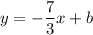
To compute y-intercept, b, plug in any of the two points into the above equation and solve for b
Let's choose point (3, -2)
Plugging x = 3 and y = -2 gives
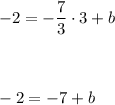
So equation of line is