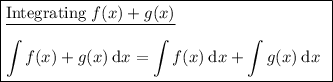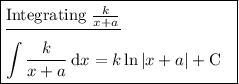Question

This is for my algebra class and this calculus stuff honestly hurts my brain, help would be appreciated

Answer 1

`\ln |x+2|+\ln |x-3|+\text{C}`

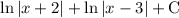
Explanation:

Fundamental Theorem of Calculus

`\displaystyle \int \text{f}(x)\:\text{d}x=\text{F}(x)+\text{C} \iff \text{f}(x)=\frac{\text{d}}{\text{d}x}(\text{F}(x))`

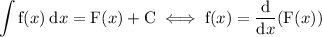
If differentiating takes you from one function to another, then integrating the second function will take you back to the first with a constant of integration.

Given indefinite integral:

`\displaystyle \int (2x-1)/(x^2-x-6)\: \text{d}x`

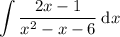
Factor the denominator:

`\begin{aligned}\implies x^2-x-6 & = x^2-3x+2x-6\\& = x(x-3)+2(x-3)\\& = (x+2)(x-3)\end{aligned}`

`\implies \displaystyle \int (2x-1)/(x^2-x-6)\: \text{d}x=\int (2x-1)/((x+2)(x-3))\: \text{d}x`

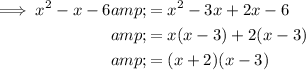
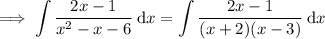
Take partial fractions of the given fraction by writing out the fraction as an identity:

`\begin{aligned}\implies (2x-1)/((x+2)(x-3)) & \equiv (A)/(x+2)+(B)/(x-3)\\\\\implies (2x-1)/((x+2)(x-3)) & \equiv (A(x-3))/((x+2)(x-3))+(B(x+2))/((x+2)(x-3))\\\\\implies 2x-1 & \equiv A(x-3)+B(x+2)\end{aligned}`

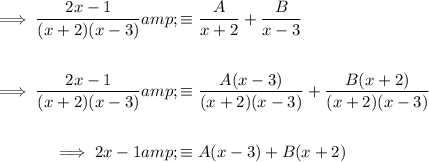
Calculate the values of A and B using substitution:

`\textsf{When }x=-2 \implies -5 =A(-5)+B(0) \implies A=1`

`\textsf{When }x=3 \;\;\: \implies 5 =A(0)+B(5) \;\;\;\;\;\: \implies B=1`

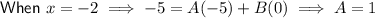
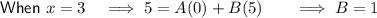
Substitute the found values of A and B into the identity:

`\implies (2x-1)/((x+2)(x-3)) & \equiv (1)/(x+2)+(1)/(x-3)`

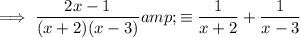
Therefore:

`\begin{aligned}\implies \displaystyle \int (2x-1)/((x+2)(x-3)) \: \text{d}x & =\int (1)/(x+2)+(1)/(x-3)\: \text{d}x\\\\ & =\int (1)/(x+2) \: \text{d}x+ \int (1)/(x-3)\: \text{d}x\\\\ & = \ln |x+2|+\ln |x-3|+\text{C}\end{aligned}`

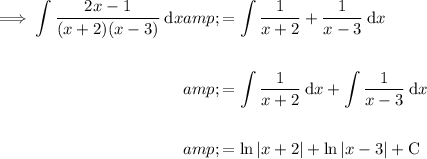
Integration rules used:

`\boxed{\begin{minipage}{6.8cm}\underline{Integrating $f(x)+g(x)$}\\\\$\displaystyle \int f(x)+g(x)\:\text{d}x=\int f(x)\:\text{d}x+\int g(x)\:\text{d}x$\end{minipage}}`

`\boxed{\begin{minipage}{4.8 cm}\underline{Integrating $(k)/(x+a)$}\\\\$\displaystyle \int (k)/(x+a)\:\text{d}x=k\ln |x+a|+\text{C}$\end{minipage}}`