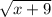
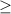
What is the inverse of (x) = √(x+9) x\geq -9 f−1(x)=(x−9)2, x≥9 f to the power of negative 1 end exponent left parenthesis x right parenthesis equals left parenthesis x minus 9 …

Question

What is the inverse of (x) =
`√(x+9)` x
`\geq` -9

f−1(x)=(x−9)2, x≥9
f to the power of negative 1 end exponent left parenthesis x right parenthesis equals left parenthesis x minus 9 right parenthesis squared, , , x is greater than or equal to 9

f−1(x)=−(x−9)2, x≤9
f to the power of negative 1 end exponent left parenthesis x right parenthesis equals negative left parenthesis x minus 9 right parenthesis squared, , , x is less than or equal to 9

f−1(x)=x2−9, x≥0
f to the power of negative 1 end exponent left parenthesis x right parenthesis equals x squared minus 9, , , x is greater than or equal to 0

f−1(x)=x2−9, x≤0

Answer 1

The inverse of
`f`, denoted
`f^(-1)`, is such that

`f\left(f^(-1)(x)\right) = x`

Given
`f(x)=√(x+9)`, we have

`f\left(f^(-1)(x)\right) = \sqrt{f^(-1)(x) + 9} = x`

Solve for
`x`.

`\sqrt{f^(-1)(x) + 9} = x`

`\left(\sqrt{f^(-1)(x) + 9}\right)^2 = x^2`

`f^(-1)(x) + 9 = x^2`

`f^(-1)(x) = x^2 - 9`

Note that
`f(x)\ge0`, so we must also have
`f\left(f^(-1)(x)\right) = x \ge 0`. This makes the third choice the correct one.