The value of y is
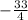 degrees.
degrees.
To find the value of y, we can use the properties of the angles in the triangle ACD and the fact that AC = BD.
1. Angle Sum Property of a Triangle:
![\[ \text{Angle CAD} + \text{Angle ACD} + \text{Angle CDA} = 180^\circ \]](https://img.qammunity.org/2023/formulas/mathematics/college/f9aqcgq2wowlvkeaqfj4e6enb15i7oa8l9.png)
![\[ 63^\circ + (3x + 45^\circ) + (y - 6^\circ) = 180^\circ \]](https://img.qammunity.org/2023/formulas/mathematics/college/ijsrh6wk1bhzk6ffcw9257ca7w804n6hjk.png)
2. Simplify and Solve for x:
![\[ 108^\circ + 3x + y - 6^\circ = 180^\circ \]](https://img.qammunity.org/2023/formulas/mathematics/college/ybnu5x712htooo639sdmx8gyb2n9ahkulk.png)
![\[ 3x + y = 78^\circ \]](https://img.qammunity.org/2023/formulas/mathematics/college/ls22a9jvk66lhxizk0vot9prcnr4ujqtfd.png)
3. Exterior Angle Property:
![\[ \text{Exterior Angle A} = \text{Angle CAD} + \text{Angle ACD} \]](https://img.qammunity.org/2023/formulas/mathematics/college/bxt2ufl79rtwo0207brwfqrxz9nvwc2vob.png)
![\[ 7x - 7^\circ = 63^\circ + (3x + 45^\circ) \]](https://img.qammunity.org/2023/formulas/mathematics/college/p4rvxow3pkl3qivh0mgmtd14a5yh3g3mgq.png)
4. Simplify and Solve for x:
![\[ 7x - 7^\circ = 108^\circ + 3x \]](https://img.qammunity.org/2023/formulas/mathematics/college/veswriofmyhs95sqnlonk32p6dx1iz2pum.png)
![\[ 4x = 115^\circ \]](https://img.qammunity.org/2023/formulas/mathematics/college/re6cb9gbspl2b4q0rszr9278sb88yh2nn5.png)
![\[ x = (115^\circ)/(4) \]](https://img.qammunity.org/2023/formulas/mathematics/college/vz7o7jzphle7doq30y7p23myhs92s1iam4.png)
5. Substitute x back into the Equation from Step 2:
![\[ 3 \left( (115^\circ)/(4) \right) + y = 78^\circ \]](https://img.qammunity.org/2023/formulas/mathematics/college/tkcz51jy314dl71m00934ct2fxcpoghjxv.png)
6. Solve for y:
![\[ (345^\circ)/(4) + y = 78^\circ \]](https://img.qammunity.org/2023/formulas/mathematics/college/rx4pkyu7bbj2hysfj7prtulbt6sjbb3ism.png)
![\[ y = 78^\circ - (345^\circ)/(4) \]](https://img.qammunity.org/2023/formulas/mathematics/college/gqi5svbx21le8y7ep99uax8aoqnqvk20lt.png)
![\[ y = (312^\circ)/(4) - (345^\circ)/(4) \]](https://img.qammunity.org/2023/formulas/mathematics/college/fpivc3vqwjuqso3pyel3efhli8z7j1oijn.png)
![\[ y = -(33^\circ)/(4) \]](https://img.qammunity.org/2023/formulas/mathematics/college/3ig325l76mdulw2j5l8emzqe5jszk97l5p.png)
So, the value of y is
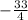 degrees.
degrees.