Answer:
x = 5, y = -11 and z = 3
As a point it is (5, -11, 3)
You can check your work by plugging these values into each of the three equations and seeing if they satisfy each equation
Explanation:
Using Gaussian elimination
Write a matrix with the coefficients and solutions
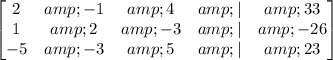
Reduce matrix to row echelon form:
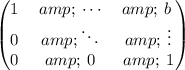
Steps
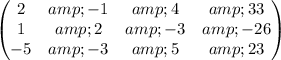
Swap matrix rows
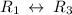
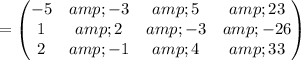
Cancel leading coefficient in row
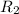 by performing
by performing
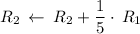
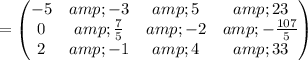
Cancel leading coefficient in row
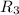 by performing
by performing
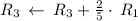
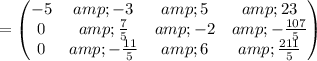
Swap matrix rows:
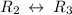
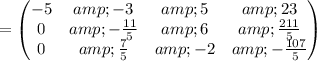
Cancel leading coefficient in row
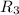 by performing
by performing
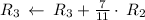
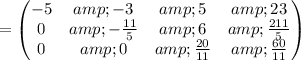
Multiply matrix row by constant:
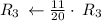
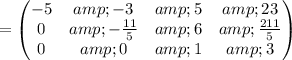
Cancel leading coefficient in row
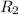 by performing
by performing
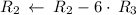
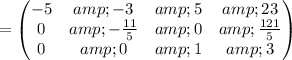
Cancel leading coefficient in row
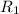 by performing
by performing
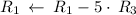
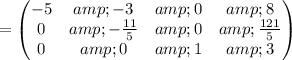
Multiply matrix row by constant:
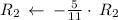
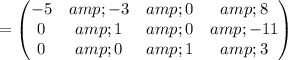
Cancel leading coefficient in row
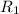 by performing
by performing
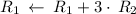
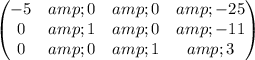
Multiply matrix row by constant :

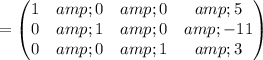
This means x = 5, y = -11 and z = 3
Other row transformation sequences are possible but as you long as you can get a matrix to row echelon form you can determine what the solution set is