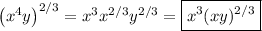It depends on what you mean "simplify". Chances are the goal here is to resolve any exponents that are improper fractions, meaning we don't want exponents larger than 1, like 4/3, for instance, but smaller than 1, like 2/3, is okay.
Now, by the distributive property of exponentiation,

Since
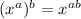 , we have
, we have
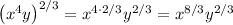
Convert the improper fraction to a mixed number.

Then we can write
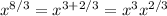
since
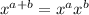 .
.
Finally, we group together the factors with the same power.