Answer:
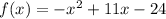
Explanation:
Well for this problem, you want to start off by writing it in factored form.
In factored form, you can represent a quadratic as:
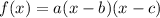 , where x=b, and x=c are zeroes of the function, since plugging them into the function makes one of the factors zero, and multiplying zero by the other factors will just give you zero.
, where x=b, and x=c are zeroes of the function, since plugging them into the function makes one of the factors zero, and multiplying zero by the other factors will just give you zero.
The "a" in front of the two factors generally defines the stretch/compression of the function.
So let's start by plugging in the zeroes into the function, and then we can solve for "a" later:
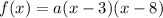
Now let's use one point on the graph, which is not a root/zero to solve for "a". It's important to not use a zero/root since if we use that point the entire thing will be zero regardless of the value of "a"
Luckily we have one point provided that is not a zero and is: (4, 4)
So let's plug it in:
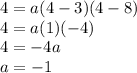
So now let's plug this into the factored form to get:
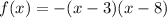
using foil to multiply these two factors you get: -[x^2 -8x - 3x + 24]
Now combine like terms
-[x^2 - 11x + 24]
distribute the negative sign
-x^2 + 11x - 24