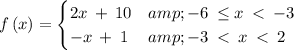Question

PLEASE HELP ASAP! I am struggling piece wise function

Answer 1

`f\left(x\right)=\begin{cases}2x\:+\:10&-6\:\le x\: < \:-3\\ -x\:+\:1&-3\: < \:x\: < \:2\end{cases}`

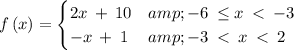
Explanation:

Looking at the graph we can see that it is a linear graph of the form

y = mx + b where m is the slope and b is the y intercept.

In one region the slope is positive and the other region it is negative

Interval 1 is -6 ≤ x < -3
How do I know that one uses a ≤ and the other uses a <?
A filled circle means that the point is included in the domain(range of x values) and therefore (≤, ≥) and an unfilled circle means it is not(<, >)

Find the slope of line in this interval
Take two points, say (-5, 0) and (-3, 4)

Slope = rise/run = (4 - 0)/(-3 - (-5) = 4/2 = 2

So slope of line is 2 and its equation in slope-intercept form is

y = 2x + b

Choose any point, plug in values, solve for b

Point (5, 0) is chosen
0 = 2(-5) + b

0 = -1 + b

or

b = 10

So equation of line in the interval (-6 ≤ x < -3) is
y = f(x) = 2x + 10

Interval 2: -3 < x < 2

We see this line intersects the y axis at y = 1

So b = 1

Equation is y = mx + 1

Choose point x = 0, y = 1 to find slope m

At x = 0, y = m(1) + 1 = m + 1

So m + 1 = 0

m = -1

So equation of this line is

y = f(x) = -1x + 1 in the interval -3 < x < 2

Putting all these together we get the piecewise function as:

`f\left(x\right)=\begin{cases}2x\:+\:10&-6\:\le x\: < \:-3\\ -x\:+\:1&-3\: < \:x\: < \:2\end{cases}`