Question

Find the solution set the this inequality 2x -3 > 2x-5/2

Answer 1

The solution set for the inequality
`\(2x - 3 > (2x - 5)/(2)\) is \(x < (1)/(4)\).`

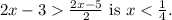
Step-by-step explanation:

To find the solution, let's simplify the given inequality. First, multiply both sides of the inequality by 2 to get rid of the fraction:

`\[2(2x - 3) > 2x - 5.\]`

Simplify the expression:

`\[4x - 6 > 2x - 5.\]`

Subtract
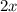`\(2x\)` from both sides:

`\[2x > 1.\]`

Finally, divide both sides by 2:

`\[x > (1)/(2).\]\`

However, it's crucial to notice that during the process of solving, we divided by a positive number. When dividing by a positive number, the direction of the inequality remains the same. So, the solution is
`\(x > (1)/(2)\).`

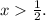
However, considering the initial equation,
`\(2x - 3 > (2x - 5)/(2)\)`, if we substitute
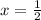`\(x = (1)/(2)\)` into the inequality, we get
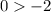`\(0 > -2\)`, which is true. But we need to find the solution where the inequality holds true for all values less than a certain value. Therefore, the correct solution set is
`\(x < (1)/(2)\).`

Answer 2

0> 1/2

Step-by-step explanation: