Answer:
-5x + 10
Explanation:
If a line 2 is perpendicular to line 1 and line 1 has slope m, then line 2 must have slope =
 which is the negative of the reciprocal of m
which is the negative of the reciprocal of m
Essentially the product of the two slopes = -1
The line
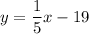
has slope of
 so the slope of line h which is perpendicular to this line must have slope = negative of reciprocal of
so the slope of line h which is perpendicular to this line must have slope = negative of reciprocal of

Reciprocal of
 is 5
is 5
Negative of reciprocal is thus -5
Equation of h is of the form
y = -5x + b where b is the y intercept, the value of y at x = 0
Since line h passes through (3, 0) we plug in these values for x and y and solve for b
0 = -5(3) + b
0 = -15 + b
15 = b (Adding 15 on both sides)
b = 15
Equation of line h is y = -5x + 15
Line g is parallel to line h. Parallel lines have the same slope so the equation for line g is
y = -5x + b (since slope of g = slope of h = -5)
Since this line passes through x = -1, y = 15 we can solve for b as before by plugging these values into the equation
15 = -5(-1) + b
15 = 5 + b
10 = b (Subtracting 5 on both sides)
b = 10
So equation of line g = -5x + 10