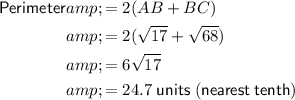Question

NO LINKS!!

Plot the points and find the perimeter and area of each polygon ​

Answer 1

11. 17.7 units

12. 24.7 units

Explanation:

The perimeter of a two-dimensional shape is the distance all the way around the outside.

To find the perimeter of a polygon, sum the lengths of its sides.

Use the distance formula to find the length of each side.

`\boxed{\begin{minipage}{4.7 cm}\underline{Distance Formula}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the two endpoints.\end{minipage}}`

Question 11

Given points:

• A = (-2, 1)
• B = (2, 5)
• C = (5, 1)

Use the distance formula to find the length of each side of ABC:

`\begin{aligned}AB & = √((x_B-x_A)^2+(y_B-y_A)^2)\\& = √((2-(-2))^2+(5-1)^2)\\& = √(4^2+4^2)\\& = √(16+16)\\& = √(32)\end{aligned}`

`\begin{aligned}BC & = √((x_C-x_B)^2+(y_C-y_B)^2)\\& = √((5-2)^2+(1-5)^2)\\& = √(3^2+(-4)^2)\\& = √(9+16)\\& = √(25)\\& = 5\end{aligned}`

`\begin{aligned}AC & = √((x_C-x_A)^2+(y_C-y_A)^2)\\& = √((5-(-2))^2+(1-1)^2)\\ & = √(7^2+0^2)\\ & = √(49)\\ & = 7\end{aligned}`

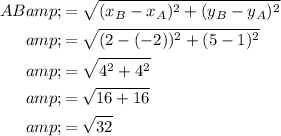
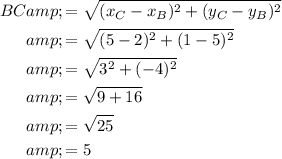
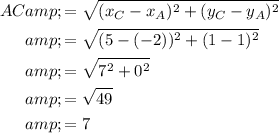
To find the perimeter, sum the sides:

`\begin{aligned}\sf Perimeter & = AB+BC+AC\\& = √(32)+5+7\\& = 4√(2)+12\\& = 17.7\;\sf units\;(nearest\:tenth)\end{aligned}`

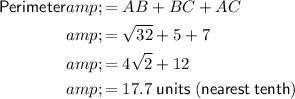
Question 12

Given points:

• A = (-3, 5)
• B = (1, 6)
• C = (3, -2)
• D = (-1, -3)

After plotting the given points, it is clear that the polygon is a parallelogram. As the opposite sides of a parallelogram are equal in length:

• AB = DC
• BC = AD

Therefore, we only need to find the length of two sides to calculate the perimeter.

Use the distance formula to find AB and BC:

`\begin{aligned}AB & = √((1-(-3))^2+(6-5)^2)\\& = √(4^2+1^2)\\& = √(16+1)\\& = √(17)\end{aligned}`

`\begin{aligned}BC & = √((3-1)^2+(-2-6)^2)\\& = √(2^2+(-8)^2)\\& = √(4+64)\\& = √(68)\end{aligned}`

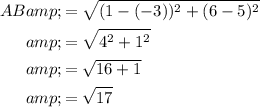
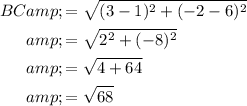
Therefore, the perimeter of ABCD is:

`\begin{aligned}\sf Perimeter & = 2(AB+BC)\\& = 2(√(17)+√(68))\\& = 6√(17)\\& =24.7\;\sf units\;(nearest\:tenth)\end{aligned}`