Question

NO LINKS!!! Please assist me part 2a

Plot the points in the coordinate plane. Then determine whether AB and CD are congruent. Explain

Answer 1

AB and CD are congruent.

Explanation:

Given points:

• A = (-4, 1)
• B = (-4, 8)
• C = (-2, -5)
• D = (5, -5)

After plotting the given points (see attachment), we can easily determine that AB is 7 units and CD is 7 units. Therefore, AB and CD are congruent.

Alternatively, as points A and B share the same x-coordinate, the length of AB is the difference between the y-coordinates:

⇒ AB = 8 - 1 = 7 units

Similarly, as points C and D share the same y-coordinate, the length of CD is the difference between the x-coordinates:

⇒ CD = 5 - (-2) = 7 units

Finally, we can prove that AB and CD are congruent by calculating their lengths using the distance formula.

`\boxed{\begin{minipage}{7.8 cm}\underline{Distance Formula}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the two endpoints.\end{minipage}}`

`\begin{aligned}\implies AB & =√((x_B-x_A)^2+(y_B-y_A)^2)\\& =√((-4-(-4))^2+(8-1)^2)\\& =√((0)^2+(7)^2)\\& =√(0+49)\\& =√(49)\\& =7\end{aligned}`

`\begin{aligned}\implies CD & =√((x_D-x_C)^2+(y_D-y_C)^2)\\ & =√((5-(-2))^2+(-5-(-5))^2)\\ & =√((7)^2+(0)^2)\\ & =√(49+0)\\ & =√(49)\\ & =7\end{aligned}`

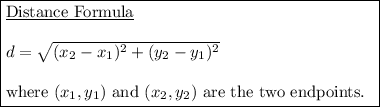
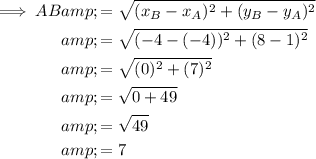
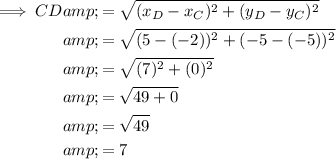
Therefore, as AB = CD, this proves that AB and CD are congruent.