Answer:
160π
Explanation:
The surface area of a right circular cylinder can be calculated using the following equation:
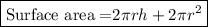 ,
,
where h is the height and r is the radius of the base of the cylinder.
We are told that the rod is 16 inches tall, therefore h = 16. We are also told that the radius of the base is 4 inches, therefore r = 4. Using this information along with the formula above, we can calculate the surface area of the metallic rod:
Surface area =

=
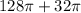
=
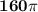
Therefore the surface area of the metallic rod is 160π.