Answer:
17 days
Explanation:
Since John starts with $500 and each day, he’ll spend $15 on lunch. This means that:
- On his first day, he’ll spend $15.
- On his second day, he’ll spend another $15 which is total spend of $30 ($15 x 2)
- On his third day, he’ll spend total of $45 ($15 x 3)
Therefore, on his nth day, he’ll spend $15n where n represents the day. The problem can be modeled into an equation of
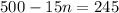 since we will be finding how many days it will take to reach $245.
since we will be finding how many days it will take to reach $245.
Then solve for n-term which we determines as the day variable:
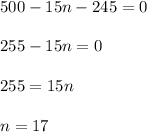
Therefore, on his 17th day, he’ll have $245. Hence, the answer is 17 days.