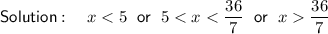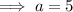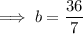Question

PLEASE HELP ME QUICK

Answer 1

`a = 5`

`b = (36)/(7)`

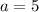
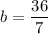
Explanation:

Given functions:

`\begin{cases}f(x)=(1)/(x-7)\\\\g(x)=(1)/(x-5)\end{cases}`

Function composition is an operation that takes two functions and produces a third function.

The given composite function
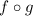`f \circ g` equals f[g(x)], which means to substitute function g(x) in place of the x in function f(x):

`\begin{aligned}\implies f \circ g (x) & = f[g(x)]\\\\& = f\left((1)/(x-5)\right)\\\\& = (1)/((1)/(x-5)-7)\\\\& = (1)/((1)/(x-5)-(7(x-5))/(x-5))\\\\& = (1)/((1-7(x-5))/(x-5))\\\\& = (x-5)/(1-7(x-5))\\\\& = (x-5)/(36-7x)\end{aligned}`

The domain is the set of all possible input values (x-values).

The domain of the composite function f[g(x)] is the set of those inputs x in the domain of g for which g(x) is in the domain of f.

The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.

Therefore, the domain of g(x) consists of all real numbers except x = 5, since that input value causes the denominator to be zero.

So x = 5 is not in the domain of the composite function.

The domain of f(x) consists of all real numbers except x = 7, since that input value causes the denominator to be zero.

So it is necessary to exclude from the domain of g(x) that value of x for which g(x) = 7.

`\begin{aligned}g(x) & = 7\\\implies (1)/(x-5) & =7 \\1 & = 7(x-5)\\1 & = 7x-35\\7x&=36\\x&=(36)/(7)\end{aligned}`

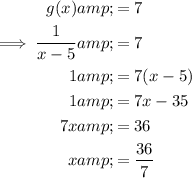
Alternatively, to find the other value of x that is not in the domain of the composite function, set the denominator of the composite function to zero and solve for x → x = ³⁶/₇.

Therefore, the domain of the given composite function is the set of all real numbers except x = 5 and x = ³⁶/₇:

Domain of the composite function

`\textsf{Solution}: \quad \textsf{$x < 5$ \;or\; $5 < x < (36)/(7)$ \;or \;$x > (36)/(7)$}`

`\textsf{Interval Notation}: \quad (- \infty, 5) \cup \left(5, (36)/(7) \right) \cup \left((36)/(7), \infty \right)`

`\textsf{As\; $5 < (36)/(7)$\; and\; $a < b$\; then}:`

`\implies a = 5`

`\implies b = (36)/(7)`