Answer:
17,640 ways
Explanation:
This is a problem in combinatorics which tells you in how many ways you can pick r items from a total of n items.
The notation for this is
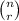 also written as C(n, r)
also written as C(n, r)
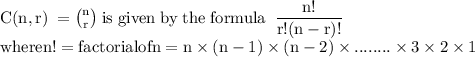
Let's deal with each of the choices
2 freshmen out of 5 freshmen.
This is C(5, 2)
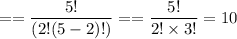
3 sophomores out of 9 sophomores
= C(9, 3)
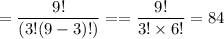
4 juniors out of 7 juniors
C(7, 4)
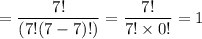
5 seniors out of 7 seniors
C(7, 5)
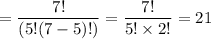
So total number of ways in which we can fill this committee
= 10 x 84 x 1 x 21
= 17,640 ways