Answer:
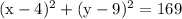
============================================================
Step-by-step explanation:
Let's find the distance from the center (4,9) to the point on the circle (-8,14)
This distance is the radius of the circle.
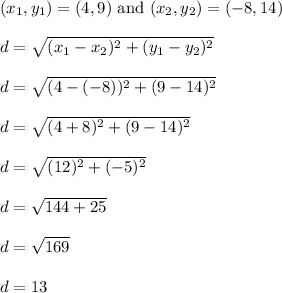
The radius of the circle is r = 13 units.
The center is (h,k) = (4,9)
So,
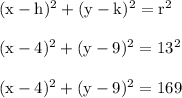
represents the equation of the circle.
You can use graphing tools like Desmos or GeoGebra to confirm. The diagrams of each are shown below as separate images.